Como seria o mundo se alguma coisa deixasse de existir? Já pensou sobre isso? Por exemplo: e se não existissem espelhos? Será que as pessoas iriam andar mais descabeladas? Será que o trânsito nas cidades ficaria ainda mais louco sem os retrovisores? E se a Lua não existisse? O que seria das marés, das histórias de Lobisomem ou do romantismo ao luar?

Mas, já que esta é uma coluna de Matemática, dê uma olhada nesse quadrado cheio de números:

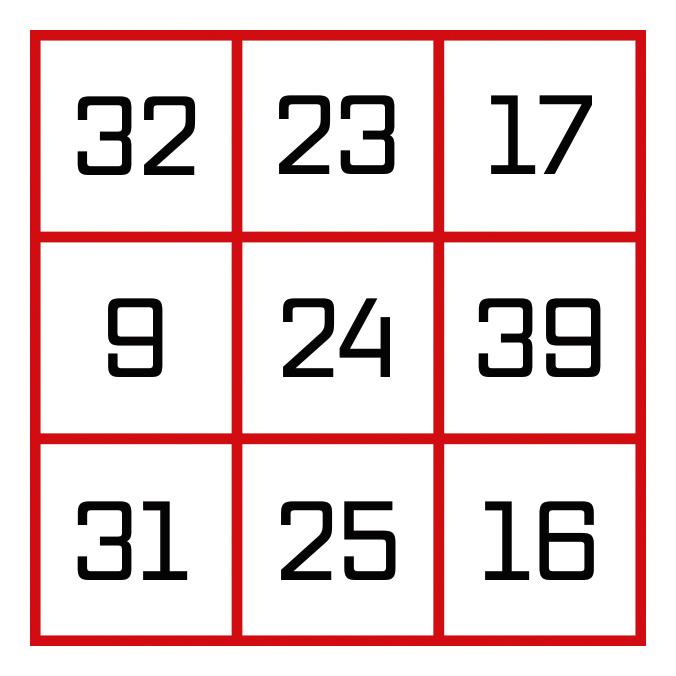
Ele tem uma coisa muito especial: se você somar os números de uma linha ou de uma coluna, até mesmo das diagonais, encontrará sempre o mesmo resultado. Por exemplo, na primeira linha temos 32, 23 e 17, a soma 32 + 23+ 17 é 72 (confira!). Na coluna do meio, temos 23, 24 e 25, a soma também é 72, e assim por diante. Quadrados assim são chamados de quadrados mágicos.

Agora imagine que, do nada… puff! Os números deixassem de existir! O quadrado mágico, que é cheio de números, ficaria assim:

Meio sem graça, não? Mas podemos colocar alguma coisa no lugar dos números para que o quadrado volte a ser interessante. Veja:

Hummm… Será que esse quadrado com essas formas geométricas dentro dos quadradinhos tem alguma coisa de especial? Pense um pouco. Pensou? Agora repare que se você juntar, por exemplo, as 3 formas da primeira linha, poderá formar um quadrado:

E se você unir as 3 formas da segunda coluna também poderá formar outro quadrado do mesmo tamanho:

E com as três formas de uma das diagonais também dá para formar outro quadrado do mesmo tamanho:

Na verdade, isso acontece para todas as formas que estão na mesma linha, na mesma coluna ou na mesma diagonal! Assim, aquela propriedade das somas do quadrado mágico com números tem uma versão geométrica que talvez seja ainda mais bacana.

É claro que, como matemático, eu não gostaria de viver em um mundo sem números. Mas, por outro lado, também como matemático, adoro pensar em mundos alternativos que às vezes nos levam a novas descobertas. E você?

Desafio: verifique se o que eu mostrei para uma linha, uma coluna e uma diagonal, realmente acontece para todas as outras linhas, colunas e diagonais.