Na hora do recreio, em uma escola no mundo da matemática, eu vi dois grupinhos que não queriam brincar juntos. Em um desses grupos estavam os quadrados e os triângulos, era o grupo das formas. No outro grupo estavam uns pontinhos, representando os números. Vendo essa separação, eu pensei: – Seria tão legal se eles pudessem brincar juntos!
Coloquei a ideia em prática! Chamei alguns quadrados e uns triângulos, e falei para os pontinhos entrarem nessas formas de uma maneira bem ordenada. (Já vou me explicar com uns desenhos.)
Então, se um número de pontinhos conseguisse preencher, sem bagunçar, um quadrado, esse número ganharia o nome de número quadrado, e se um número de pontinhos conseguisse preencher, sem bagunçar, um triângulo, ele ganharia o nome de número triangular.
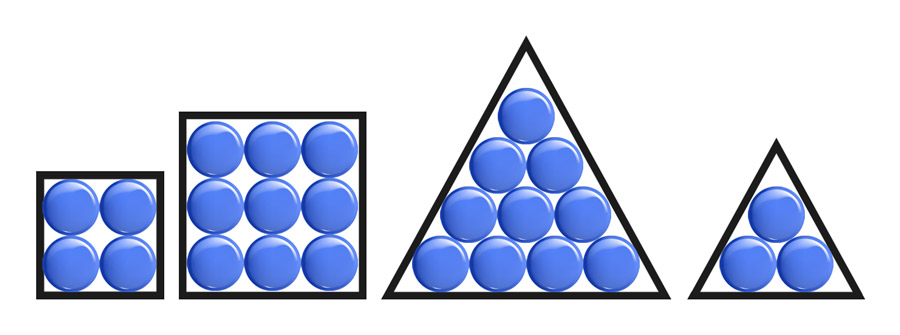
No mundo da matemática, uma das maiores diversões é fazer perguntas meio malucas e tentar respondê-las. Então, vamos lá: – Será que um número pode, ao mesmo tempo, ser quadrado e também triangular?
À primeira vista pensei que a resposta seria não, já que um quadrado nunca pode ser um triângulo. Mas…,a pergunta não é bem essa! A pergunta é se existe um número que é quadrado e também triangular.
O número 1 se agitou todo e disse: – Sou eu, sou eu, eu sou o único número que é quadrado e triangular!
Realmente, o número 1 é mesmo quadrado e triangular, veja a figura. Mas será que ele é o único?
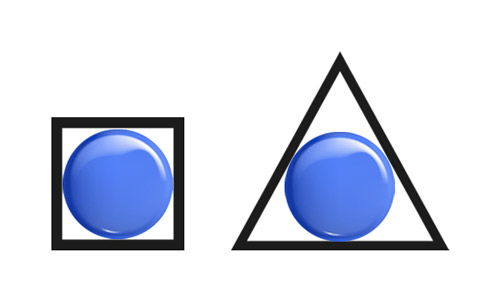
Talvez por ser o número 1, ele tenha essa mania de pensar que é sempre o grande vencedor. O que você acha?
Fui até a cozinha e peguei grãos (crus) de feijão, e comecei a investigar. Eu fiz assim: fui arranjando os feijões em quadrados e encontrei os primeiros números quadrados: 1, 4, 9, 16, 25, 36.
Peguei, então, 4 feijões e tentei arranjá-los em forma triangular. Não deu! Tentei a mesma coisa com 9 feijões, e nada. Depois, com 16 e 25. Não deu, não deu. Eu já estava desistindo quando uma voz interior me disse: – Tente um pouco mais!
E não é que com 36 feijões deu certo! Olha só!
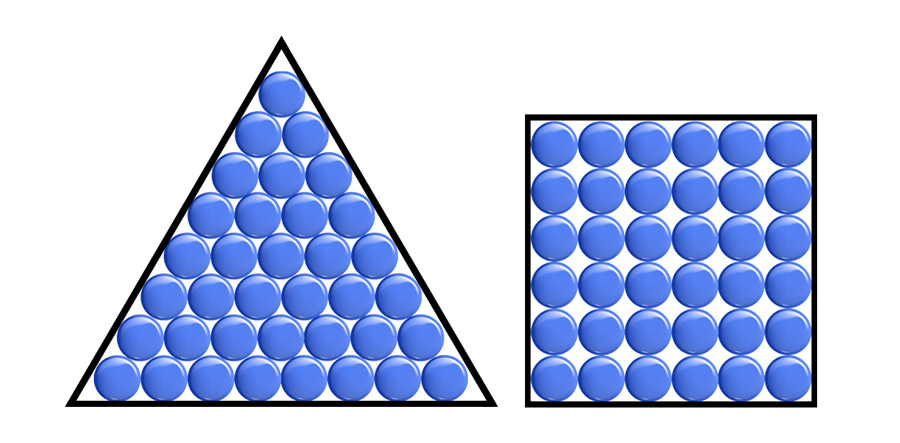
E agora? Será que existem mais desses números quadrados triangulares? A resposta é sim, existem infinitos! Só que esse método do feijão não é muito bom para encontrá-los. Por exemplo, para encontrar o próximo, você precisaria de 1.225 grãos! E para o seguinte seriam necessários mais de 40 mil grãos!
Bem, o recreio acabou, e felizmente consegui ver as formas e números brincando juntos. Quando isso acontece, a matemática fica sempre mais bonita.

Pedro Roitman,
Instituto de Matemática,
Universidade de Brasília
Sou carioca e nasci no ano do tricampeonato mundial de futebol – para quem é muito jovem, isso aconteceu em 1970, século passado! Enquanto fazia o curso de Física na universidade, fui encantado pela Matemática. Hoje sou professor.
Matéria publicada em 21.10.2019