Nas férias, meu filho e uma amiga estavam de bobeira em casa e decidi propor um desafio a eles. Sendo férias, o prêmio seria um doce! Claro que eles ficaram bem animados. 

O desafio era assim: primeiro, desenhei um triângulo, que subdividi em triângulos menores. Em seguida, escolhi três cores e pintei cada vértice do triângulo original com uma delas. Ficou assim:

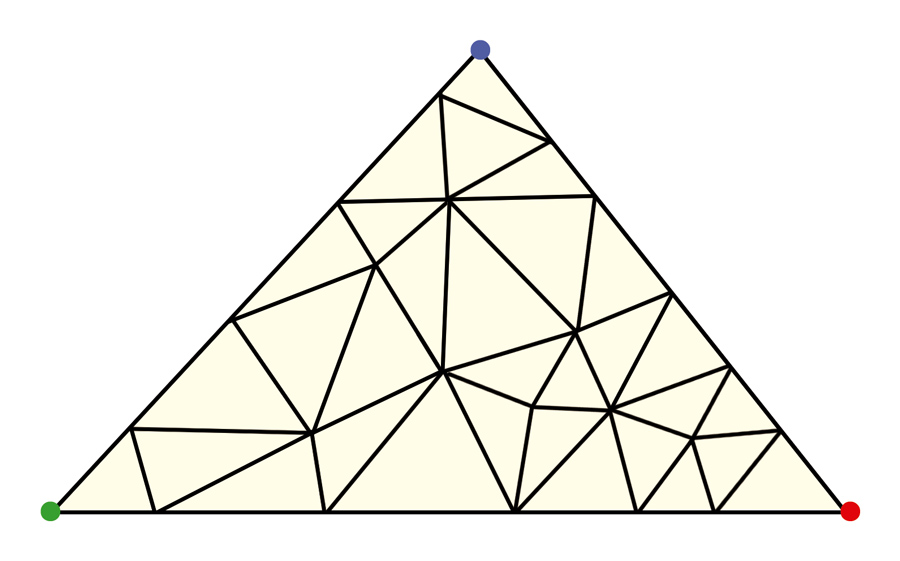
Pedi, então, para as crianças pintarem os vértices dos triângulos menores, que estão nos lados do triângulo original, usando apenas as cores dos vértices já pintados nas extremidades desse lado. Por exemplo: o lado maior do triângulo na figura acima tem extremidades verde e vermelha, logo, teriam que colorir os outros vértices nesse lado usando apenas essas duas cores. E fizeram assim:

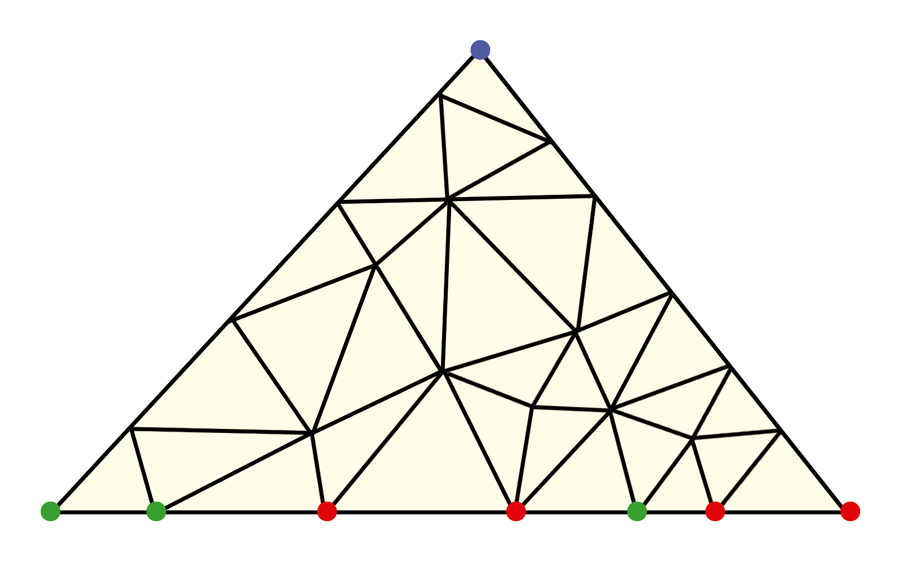
Para colorir os outros vértices que estão nos lados do triângulo grande, a regra era a mesma, com um pequeno detalhe: era proibido formar um triângulo tricolor, ou seja, com vértices pintados com três cores diferentes. Eles disseram: “Beleza!” E deixaram o triângulo assim:

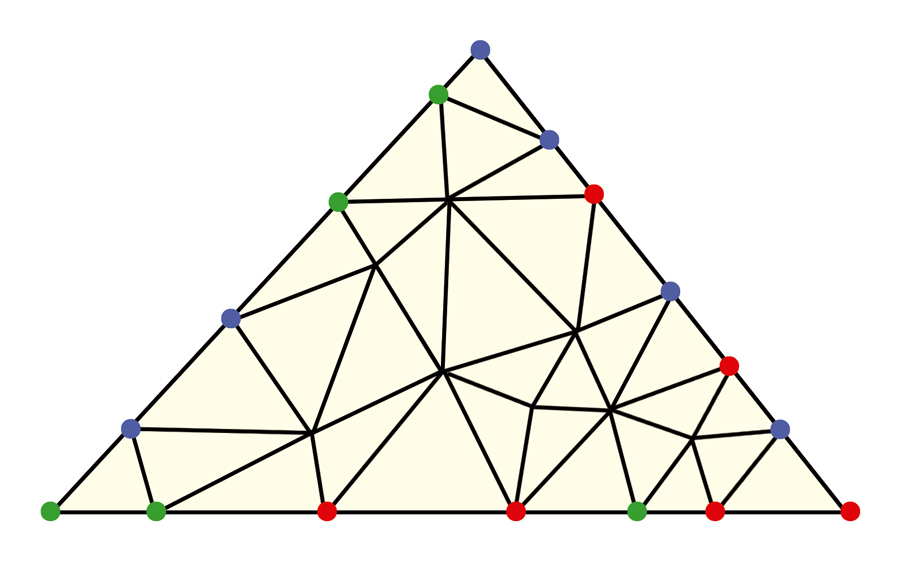
Aí, eu disse: “Podem colorir o restante dos vértices do jeito que quiserem. Se conseguirem colorir todos sem formar um triângulo tricolor, ganham a aposta”.

Com água na boca, pensando no doce, foram colorindo os vértices sem formar um triângulo tricolor, até que sobrou um pra terminar. Repare:

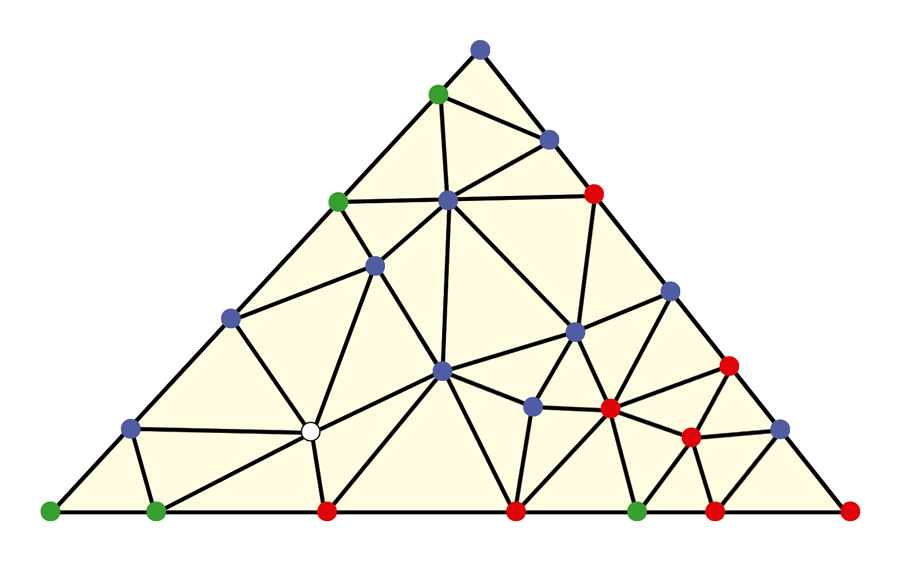
Elas perceberam que, colorindo esse vértice com qualquer uma das três cores, formariam um triângulo tricolor. Então, eu disse que poderiam tentar outra vez. Refizeram tudo outra vez e mais outra e mais outra… até que começaram a gritar: “É impossível! É impossível!”.

Você que está acompanhando esta história se anima a reproduzir a figura inicial e tentar? Se fizer isso, não vale ler agora o final deste texto, porque vai perder a graça!

Bem… na verdade, é impossível mesmo. A gente pode começar com qualquer triângulo, subdividir ele formando triângulos menores do jeito que a gente quiser, colorir a borda do triângulo maior, respeitando aquela regrinha, e sempre vai aparecer um triângulo tricolor quando a gente for colorir os outros vértices. Sempre!

Pensei que as crianças ficariam zangadas quando revelei que o desafio era impossível de solucionar, mas elas se divertiram com a pintura e ainda acharam interessante quando contei que foi um matemático alemão chamado Sperner que havia usado a matemática para provar que sempre apareceria um triângulo tricolor. É claro que, pelo espírito esportivo, cada um ganhou um doce!