Para começar essa história, apresento a você os personagens principais. Aqui temos os números hexagonais, ou melhor, os quatro primeiros:

As bolinhas são todas idênticas e estão arranjadas nesse formato de hexágono, representado os números: 1, 7, 19 e 37.

Agora vamos às espaçonaves cúbicas, que são formadas por cubinhos:

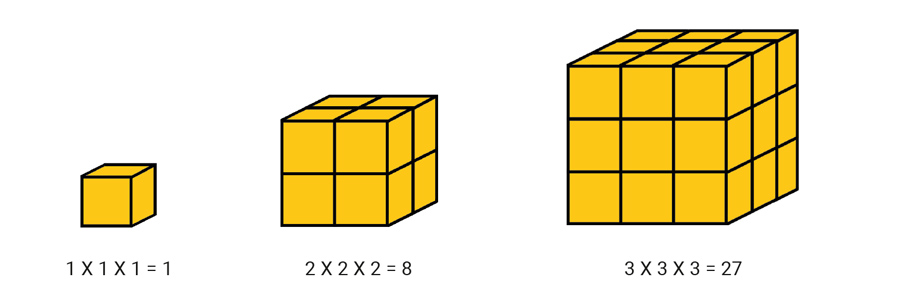
Confira o número de cubinhos que forma cada espaçonave e guarde o seguinte: em cada cubinho cabe exatamente uma bolinha.

Agora vem a história! Um certo planeta de uma galáxia distante estava prestes a explodir. Os habitantes, as bolinhas que formavam os 10 primeiros números hexagonais, receberam duas opções para escapar da trágica explosão…

Primeira opção: escolher uma única espaçonave cúbica para encher com as bolinhas. Mas, se escolhessem uma espaçonave com um número de cubinhos diferente do número de bolinhas, não conseguiriam decolar e… bum! Ou seja: para que as bolinhas conseguissem escapar, teria que existir uma espaçonave cúbica em que coubesse exatamente a soma dos 10 primeiros números hexagonais.

Segunda opção: salvar apenas metade das bolinhas com outro tipo de espaçonave.

Talvez a resposta para o dilema pareça simples: bastaria contar o número total de bolinhas que formam os dez primeiros números hexagonais. Se o resultado fosse um número cúbico – algo do tipo 1x1x1 = 1 ou 2x2x2 = 8 ou 3x3x3=27 ou 4x4x4 = 64 etc. –, então bastaria escolher a primeira opção. Se o número não fosse cúbico, pegariam a segunda opção, bem triste é verdade, em que só metade das bolinhas conseguiria se salvar.

Para matar sua curiosidade: os dez primeiros números hexagonais são 1, 7, 19, 37, 61, 91, 127, 169, 217 e 271 e a soma deles, verifique, é 1.000 (10x10x10).

Acontece que as bolinhas não sabiam contar. Elas pensavam visualmente! Vou ser sincero e dizer que não sei bem como elas resolveram o problema. Devem ter pensado em algo parecido com essas figuras, que mostram como ver a solução se o número de bolinhas fosse a soma dos três primeiros números hexagonais:

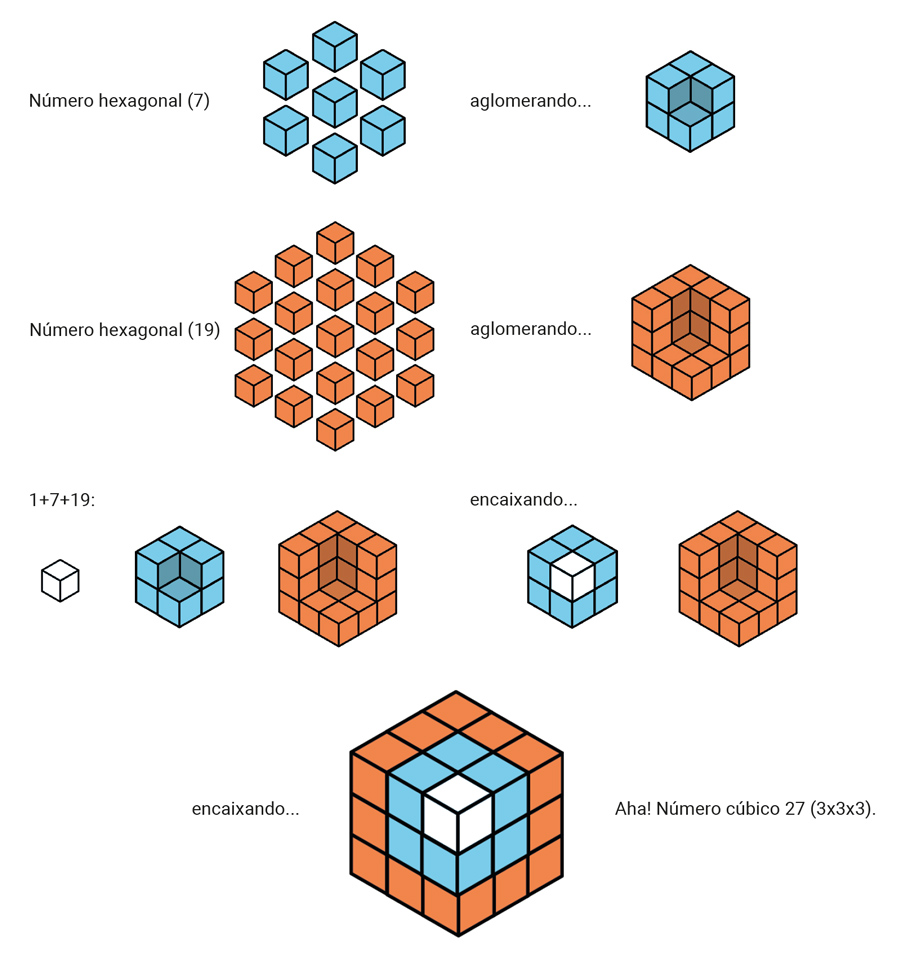
Para os 10 primeiros números, a ideia seria a mesma. Será que você descobriu por que as bolinhas escolheram a primeira opção e conseguiram sobreviver? Será que pensar visualmente é uma boa alternativa?