A maioria das pessoas poderia jurar que matemáticos e matemáticas sempre são apaixonados por fazer contas. Mas a verdade é que muitos, talvez a maioria, detestam. O que acontece é algo parecido com o carnaval, a festa que mais simboliza o Brasil: nem todos os brasileiros gostam. Mas, então, se há matemáticos e matemáticas que não gostam de fazer contas, do que eles gostam?  

Eu, como matemático, palpito que gostam de fazer conexões, de ligar duas coisas que aparentemente não tem nada a ver uma com a outra. Aceita acompanhar um desafio que serve como exemplo? Lá vai!

Vamos chamar de A o número de moedas necessárias para fazer um arranjo triangular, com cada lado do triângulo tendo 4 moedas (veja a figura). E vamos chamar de B o número de duplas que podemos formar num grupo de 5 pessoas.

Agora o desafio: Qual é maior? Será que é o número A? Será que é o número B? Ou será que eles são iguais?

As pessoas que gostam de contas iriam contar para achar o valor de A, o valor de B, para então poder dizer quem é maior, ou se A e B são iguais. Já o pessoal que gosta de fazer conexões, poderia imaginar uma fileira adicional no triângulo de moedas, veja na figura.

Essa fileira adicional teria 5 moedas, e a gente pode pensar que elas representam as 5 pessoas do tal grupo. Agora imagine uma dupla de pessoas, ou seja, duas moedas laranjas da fileira adicional, e imagine também linhas vermelhas ligando essas duas moedas a uma azul, como nesta figura: 

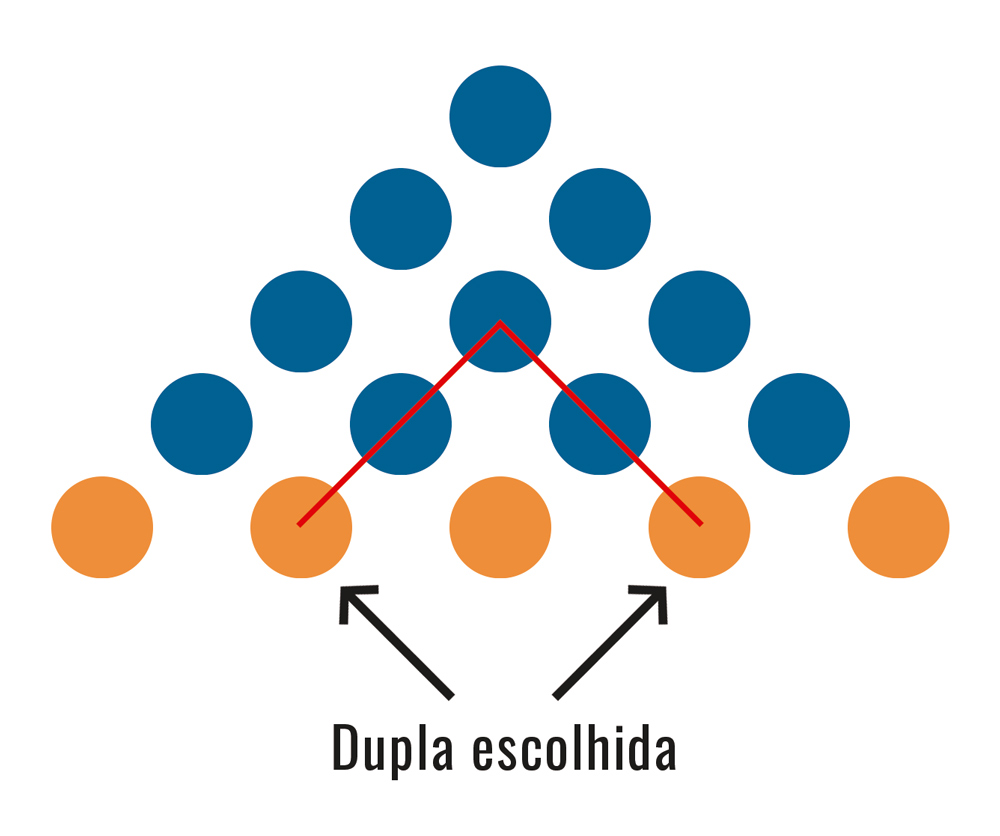
As linhas vermelhas se cruzam em uma única moeda do arranjo triangular original, certo? Mas isso vale para cada dupla de moedas escolhida. Veja mais um exemplo na próxima figura:

Assim, a cada dupla da fileira adicional, associamos uma moeda do arranjo original. E, claro, podemos reverter esse processo: começando com uma moeda do triângulo original e traçando as retas vermelhas diagonais, podemos encontrar uma dupla da fileira adicional.

Resumindo: para cada dupla de moedas da fileira adicional temos uma moeda do triângulo de moedas azuis, e vice-versa. Portanto, o número A é igual ao número B! E conseguimos responder isso sem precisar saber quanto é A e quanto é B. Driblamos as contas!

Talvez você considere mais rápido e simples contar para achar o valor de A e B. Tudo bem!  Mas note que essa ideia de imaginar as linhas vermelhas e conectar cada moeda azul com uma dupla de moedas laranjas também funcionaria da mesma maneira, se o lado do arranjo triangular tivesse, digamos, 1.000 moedas e se tivéssemos duplas em um grupo com 1.001 pessoas. Nesse caso, contar as moedas e o número de duplas seria um trabalhão!

Então, será que é mesmo possível amar a matemática sem necessariamente ter uma paixão pelas contas? Que tal conversar sobre essa pergunta com amigos, familiares e também com professores e professoras da sua escola?