Com autorização prévia do meu filho, resolvi fazer uma brincadeira na festa de aniversário dele. Nada demais, apenas um pai querendo participar da festa, certo? Errado! Acredite, nada é mais arriscado para um pai do que fazer uma brincadeira de matemática em uma festa de aniversário do próprio filho.
Aconteceu assim… Arranjei seis potes idênticos e, em cada um deles, coloquei cinco bombons que poderiam ser de 2 sabores diferentes: amêndoas ou cebola. Eles foram divididos assim:
E assim por diante, até chegarmos ao sexto pote, com cinco bombons de cebola e nenhum de amêndoas. Detalhe: a embalagem e aparência dos bombons era exatamente a mesma, só dava para descobrir o sabor experimentando mesmo.
Eu então fiquei vendado e escolhi aleatoriamente um dos potes, abri, peguei um bombom qualquer e coloquei na boca. Para a minha felicidade, não peguei um bombom de cebola, mas sim um de amêndoas delicioso. E enfim fiz a minha pergunta aos convidados:
– Se eu pegar outro bombom deste mesmo pote, tenho mais chance de pegar um de amêndoas, um de cebola, ou as chances são iguais?
Uma das convidadas respondeu:
– Acho que as chances são iguais, pois você pegou, de um pote aleatório, um bombom qualquer. Então, como tudo é pura sorte, as chances devem ser iguais!
Um outro convidado, usando os potes, argumentou mais ou menos como eu irei ilustrar com as figuras abaixo, nas quais bolinhas pretas representam bombons de amêndoas e as brancas, os de cebola.

Dos seis potes, certamente não escolhi o que só tem bolinhas brancas (sabor cebola), já que tirei do pote escolhido uma bolinha preta (sabor amêndoas). Sobram então cinco potes, certo? Agora, tirando uma bolinha preta de cada um desses cinco potes, ficamos assim:

O convidado então argumentou mais ou menos assim: como há o mesmo número de bolinhas brancas e pretas na figura acima, então a chance de escolher uma bolinha branca ou uma preta seria a mesma, certo?
Antes de continuar a leitura, que tal pensar um pouquinho para ver se você concorda com os argumentos desse convidado?
Na verdade, ele se enganou, e há muito mais chances de pegarmos um bombom com amêndoas do que um de cebola, o que surpreende muita gente! Repare…
Vamos supor que, em vez de cinco bolinhas em cada um dos seis potes, tenhamos duas bolinhas em três potes. O problema é o mesmo, apenas reduzi o número de bolinhas e potes para ficar um pouco mais fácil.
Note que dos três potes possíveis, podemos descartar como sendo o pote escolhido o que tem apenas bolinhas brancas. Restam então apenas dois potes: um deles com uma das bolinhas pretas e o outro com uma preta e outra branca.
Para esses dois potes, há três maneiras distintas de retirarmos uma bolinha preta. Veja:
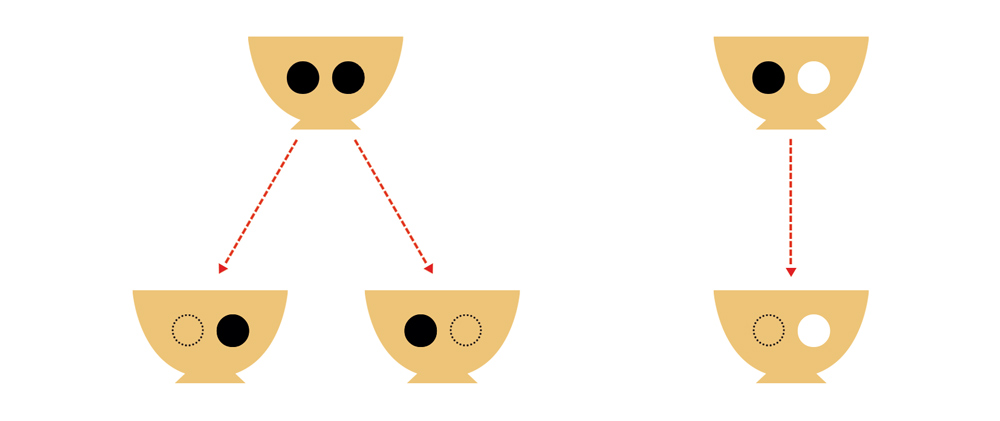
Em duas dessas maneiras, o que resta é uma bolinha preta, enquanto na outra resta uma bolinha branca. Assim, se formos retirar uma segunda bolinha, há muito mais chances (o dobro) de tirarmos uma bolinha preta, ou seja, um bombom de amêndoas.
Desafio: tente resolver esse problema para quatro potes com três bolinhas em cada; depois, para cinco potes com quatro bolinhas em cada; até chegar ao problema original da festa com seis potes e cinco bolinhas em cada. O resultado é sempre o mesmo: a chance de pegarmos um bombom de amêndoa é o dobro da chance de pegarmos um de cebola! Ainda bem, né?

Matéria publicada em 04.10.2024