Quando alguém diz ‘infinito’, o que vem à sua cabeça? Algo que não acaba mais, que não tem fim? Sabia que essa ideia de pensar em ‘coisas que não têm fim’ pode nos levar a conclusões surpreendentes? Para começar: Será que existe algo no mundo que realmente não tenha fim? Será?

De fato, existem coisas que parecem impossíveis de contar. Podemos, por exemplo, tentar contar todos os grãos de areia da Terra ou todas as estrelas da Universo? Sabemos que há ‘muuuitos’ grãos de areia e ‘muuuitas’ estrelas. Mas será que, se fossemos capazes de contá-los, algum dia chegaríamos a um fim?

Filósofos, matemáticos e físicos pensam nisso sempre. Eles tentam, inclusive, entender o Universo, especialmente sobre espaço e o tempo, por meio da matemática e dos números. E para entender a ideia de infinito, de algo que não tem fim, os matemáticos usam os números.

Vamos pensar…

Qual é o maior número que você consegue imaginar? Será que existe um número maior que todos os outros? Por mais que a gente pense em um número muito grande, é sempre possível pensar em outro número maior ainda. Pensando assim, o conjunto dos números naturais (representados na matemática pela letra N) não tem fim. São eles: N = { 1, 2, 3, 4, …} e assim por diante.
E se pensarmos em um número par (representados na matemática pela letra P)? É sempre possível pensar em outro número par maior ainda. Portanto, o conjunto dos números pares também não tem fim: P = { 2, 4, 6, 8, …}

Assim, os números naturais e os números pares são exemplos de conjuntos infinitos. Mas, ao mesmo tempo, o conjunto dos números pares está dentro do conjunto de números naturais. Então, será que há mais números naturais do que números pares? Será que um é mais infinito que o outro? Nossa! Você esperava por essa?

Mais ou menos infinito?

Se concordarmos que o conjunto de números naturais é mais infinito que o de números pares, significa que existem conjuntos infinitos maiores que outros. Se discordarmos, estamos dizendo que o conjunto de números pares pode caber inteiramente dentro do conjunto de números naturais e, ao mesmo tempo, tem a mesma quantidade de elementos.

Uma forma de ter certeza que dois conjuntos têm a mesma quantidade de elementos é ligá-los um a um, de forma que não sobre nenhum elemento de nenhum dos dois lados. Veja a figura a seguir:

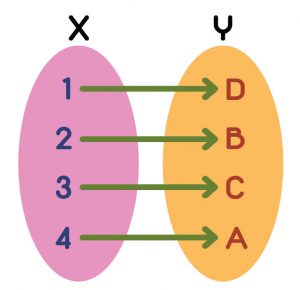
Dois conjuntos têm a mesma quantidade de elementos se for possível ligar seus elementos um a um, mas nenhum elemento pode sobrar em nenhum dos dois lados.

Se aplicarmos essa mesma ideia aos conjuntos dos números naturais e dos números naturais pares, percebemos que é possível alinhá-los e ligar seus elementos de tal forma que a cada número natural corresponda um único par e a cada número par corresponda um único número natural, sem que sobre nenhum número em nenhum dos dois conjuntos. Cada número natural deve corresponder ao seu dobro. Veja na figura:

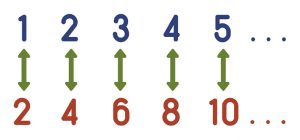
Existem tantos números naturais quantos números pares

Isso quer dizer que os conjuntos de todos os números naturais e dos números pares têm a mesma quantidade de elementos – embora um esteja inteiramente dentro do outro! Essa é a maneira dos matemáticos dizerem que algo ‘não tem fim’!

Um hotel infinito

Para explicar melhor ainda a ideia de infinto, no século 20, o matemático alemão David Hilbert usou um exemplo que ficou
muito conhecido: o Hotel de Hilbert. Mas, você precisa soltar a imaginação para pensar nesse hotel.
O lugar tem infinitos quartos. Mas, mesmo assim, esse hotel está lotado! Oi? Pois é! Mesmo com infinitos quartos, não existe
Um hotel com infinitos quartos nunca está lotado. nenhum vago. É claro que no mundo real não pode existir um hotel assim. Trata-se apenas de algo inventado por Hilbert para explicar o conceito matemático de infinto. Veja a figura a seguir:

Hilbert e o hotel com infinitos quartos.

Viajou na imaginação? Então, vamos lá! Chegou um novo hóspede procurando uma vaga. Para encontrar essa vaga, o gerente do Hotel de Hilbert pede que o hóspede do quarto 1 se mude para quarto 2, que o  hóspede do quarto 2 se mude para o quarto 3, e assim por diante. Veja a figura:

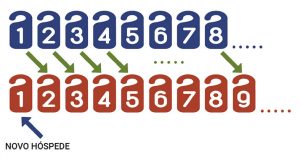
Um hotel com infinitos quartos nunca está lotado.