Organizar pode ser uma brincadeira que ajuda nas descobertas
A história do ponto rebelde
No reino da geometria, um ponto rebelde foi condenado a viver sozinho para sempre dentro de um triângulo equilátero (em que todos os lados têm o mesmo tamanho). A rebeldia do ponto funcionava assim: quando recebia uma ordem com a qual não concordava, ele simplesmente ficava imóvel e se recusava a obedecer.
Uma conselheira real, segura de que um certo grau de rebeldia poderia ser bom para o mundo, decidiu dar uma chance ao ponto aprisionado. E foi falar com ele:
– Hoje é seu dia de sorte! Ganhará a liberdade se conseguir resolver um enigma.
O ponto, se tivesse olho, olharia desconfiado. A conselheira continuou:
– Se um dos lados do triângulo que te aprisiona fosse o chão, você teria uma altura com relação a esse chão, certo? Mas, como qualquer dos lados poderia ser o chão, então temos três alturas, uma para cada lado. Veja a figura: cada altura tem a mesma cor do chão correspondente.
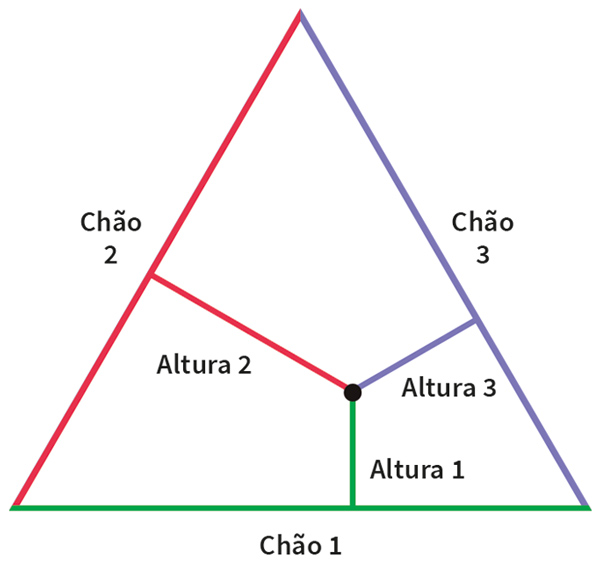
E ela disse mais:
– Senhor ponto rebelde, o desafio é encontrar o lugar em que a soma das três alturas é a menor possível.
Note que as três alturas mudam dependendo do local do ponto, veja a figuras:
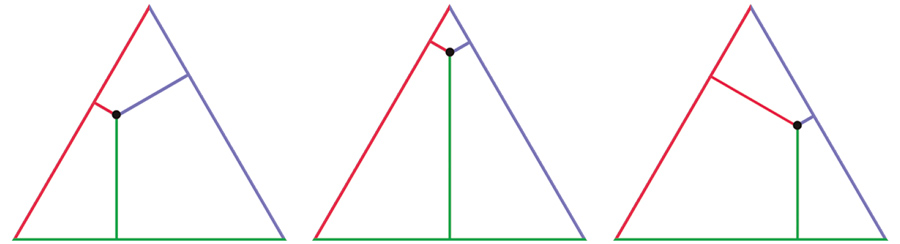
O natural seria que o ponto se mexesse, explorasse as possibilidades, até encontrar o local onde a soma das três alturas é a menor possível, certo? Mas ele ficou paradão onde estava. Isso tinha cara, cheiro e gosto de rebeldia, mas será que era? Parecia que ele se recusava a participar do desafio ao permanecer imóvel.
A conselheira então fez sinal de que ia embora decepcionada, quando então, finalmente, o ponto disse:
– Espere um pouco! Aqui onde estou é a solução do enigma. Na verdade, eu poderia estar em qualquer local dentro do triângulo! Para todos os locais a soma das três alturas é sempre a mesma, não muda! É sempre igual à altura do triângulo que me aprisiona.
A conselheira ficou surpresa e feliz com a resposta do ponto, e ele conquistou a sua liberdade.
Aqui vai uma explicação a respeito da resposta do ponto:
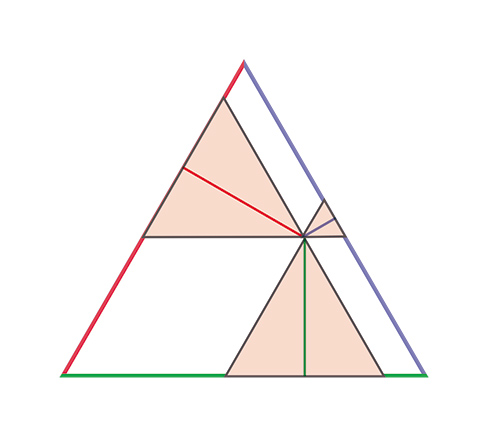
A figura acima mostra que sempre podemos imaginar três triângulos equiláteros menores dentro do triângulo maior, certo? Agora imagine que o triângulo menor desliza, indo para cima, até ficar assim:
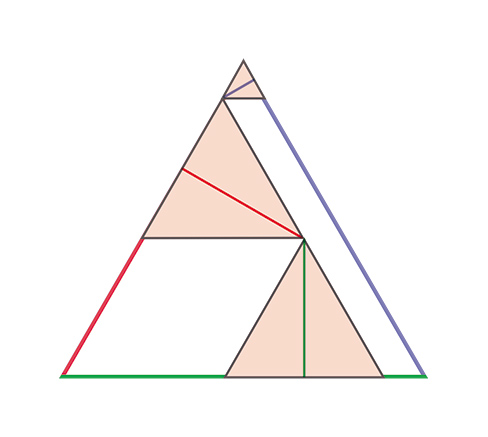
Pra terminar, girando dois triângulos em torno dos seus centros, ficamos assim:
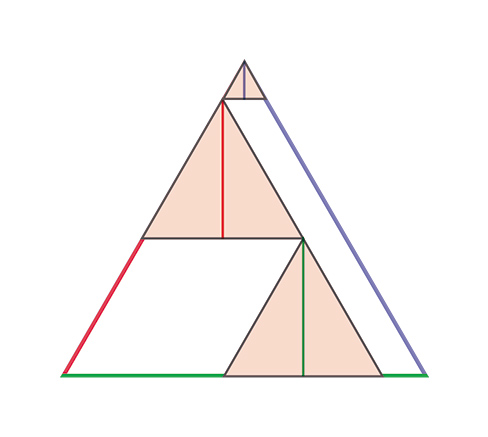
Gráfico Marina Vasconcelos
E agora, dá para ver que a soma dos segmentos verticais (o azul, o verde e o vermelho) é exatamente a altura do triângulo equilátero que aprisionava o ponto?
Duvide de mim e desenhe um triângulo equilátero, coloque um ponto dentro em qualquer lugar e refaça o que acabamos de apresentar, para ter certeza de que funciona!
Ah! Só vale ficar parado como o ponto rebelde se tiver entendido tudo!

Pedro Roitman,
Instituto de Matemática,
Universidade de Brasília
Sou carioca e nasci no ano do tricampeonato mundial de futebol – para quem é muito jovem, isso aconteceu em 1970, século passado! Enquanto fazia o curso de Física na universidade, fui encantado pela Matemática. Hoje sou professor.
Matéria publicada em 02.05.2023
COMENTÁRIOS
Envie um comentário
admin
CONTEÚDO RELACIONADO

Que comecem os Jogos! E o respeito à natureza
Qual a mensagem que os Jogos Olímpicos de 2024 querem passar ao mundo?




Victor Tavares
Oi meu nome é Victor Tavares eu queria saber como que vocês sabem tantãs coisas
Publicado em 12 de maio de 2023
vieira e yasmin
Olá, somos da Escola Estadual Nayme Cardim, somos do 5 ano B, adoramos a matéria sobre o “Ponto Rebelde”
achamos muito legal amamos kk.
Publicado em 16 de maio de 2023
PHIETRO
Eu amei explicação, eu amo sólidos geométrico!!
Publicado em 25 de maio de 2023
VITORIA
MUITAS COISAS QUE APARECEU EU NÃO SABIA MUITO. OBRIGADA POR TIRAR MINHAS DÚVIDAS 0 SEU CONTEUDO FOI MUITO BOM PARA MIM.
Publicado em 25 de maio de 2023