Criatividade e imaginação também valem na hora de pensar matematicamente

Você já ouviu a expressão “é preciso pensar fora da caixinha”? Significa que vale a pena usar a criatividade ou um ponto de vista original para tentar resolver um problema complicado. Vamos ver um exemplo de como esse tipo de coisa acontece na matemática?

Olhe para o tabuleiro da figura a seguir. Ele tem a forma de um hexágono e está dividido em muitos triângulos todos com o mesmo tamanho e forma.

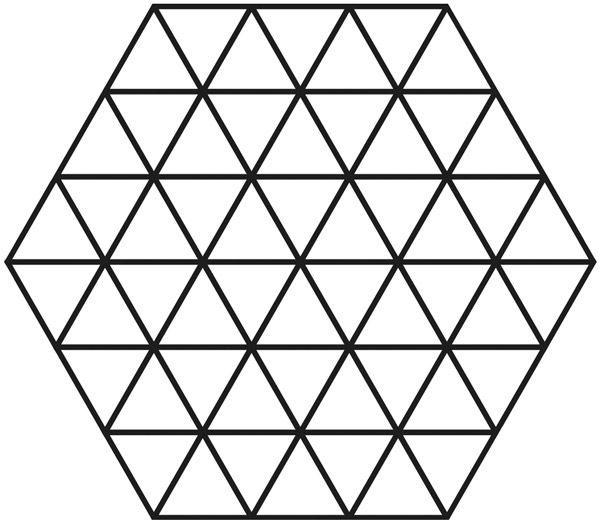
Gráficos Marina Vasconcelos